Disclaimer: This post is heavily referenced from Taleb’s book Fooled By Randomness Part I Chapter 3. It is not to be construed as financial advice and only written for educational purposes.
This might sound mind numbing or ridiculously counter intuitive. But the following is the tendency that we have observed time and time again multiple times. People seem to almost always get thrown off by short term (day to day or even minute to minute) price fluctuations when they invest.
But perhaps have we taken a moment to ask ourselves:
Out of the pluses and minuses of price that we see on a regular (daily basis), what is considered to be noise*?
What is considered to be information* or signal or meaning?
* Noise means it is something you should ignore; information is something you should pay attention to.
This writing is my attempt to shed light on how we could have a clearer picture.
Let’s start from the basics
Suppose we choose to invest in a hypothetical asset that has an expected return of 15% per annum.
I know IDX composite (in Feb 2025) is hammered immensely by a lot of people, but if you look at the Compounded Annual Growth Rate (CAGR) since inception, it is around 12%. Hence, 15% is a reasonable assumption and expectation of returns per annum of a fictional investible asset.
Now suppose the volatility of the asset is 10%. 15% is a respectable annual return, so it follows that the 10% volatility is the price we pay.
Translation: it means the asset price from time to time can go up and down in such a way that deviation from the actual return you get is 10% (it could be 5% on the lower side of the spectrum or 25% on the higher side of the spectrum).
Extra translation: remember your expected return (15%) is not equal to your actual returns. To wit, below is an illustration that might help.
Introducing a little bit of middle school math
The information above is great in theory. But even with the translation and illustration, what does it mean?
Actual returns is not equal to expected returns? Yes.
So even if I expect to have 15% yearly, I can have -80% returns right over multiple years right?
Yes, although given the information above, very very unlikely. You can win at a casino one time, but are you likely to win at a casino over and over and over again over multiple years?
To explain this question in a clear manner, recall Normal Distribution we used to learn in SMP. We can call it Gaussian Distribution as well if you want to impress some lady/lad during Valentine’s 🙃
I won’t go into the formal definition and notation (calculating the pdf and cdf unnecessarily). But let’s just have an intuitive picture on this. The simple intuition is as such:
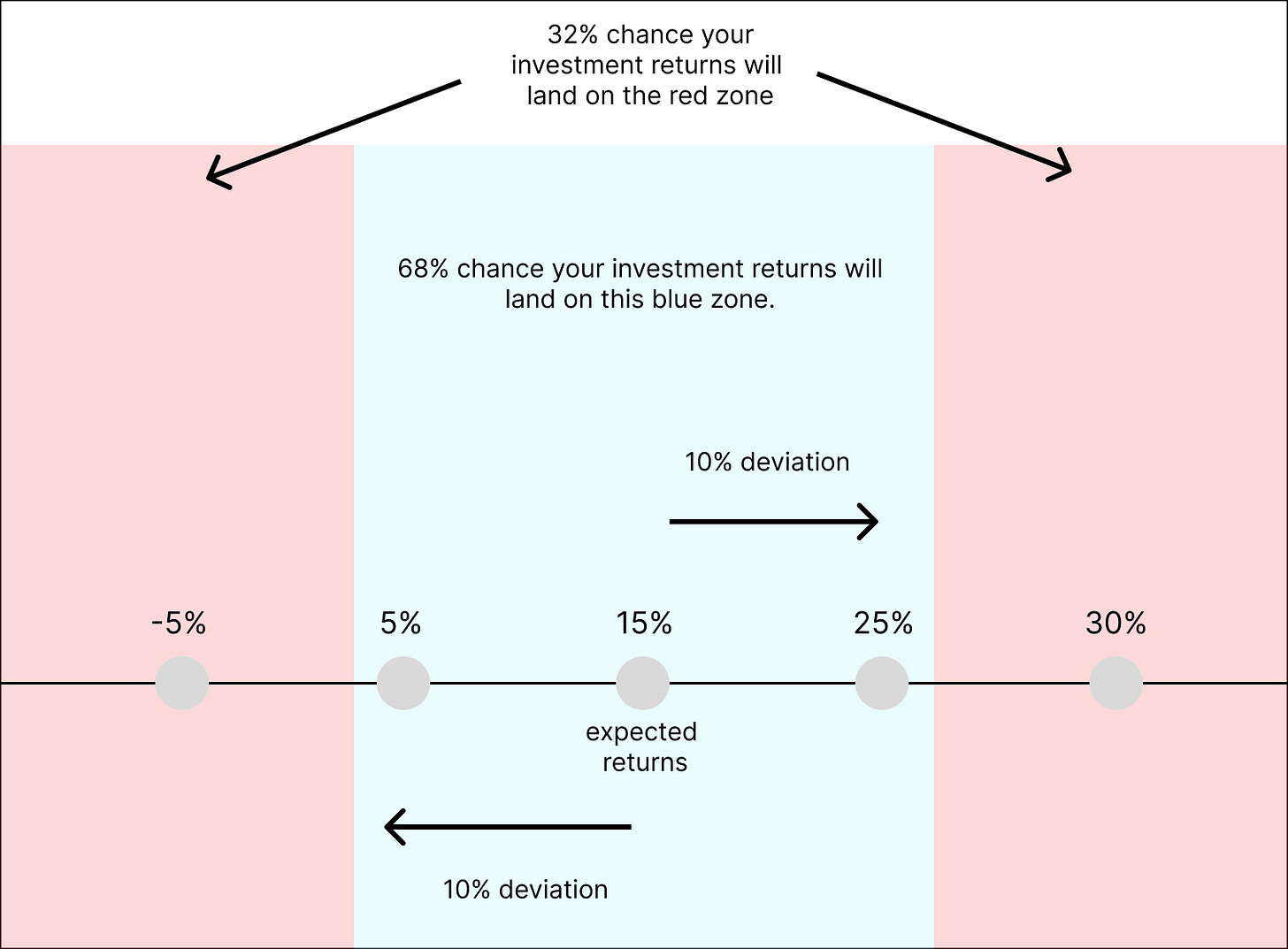
Imagine, you investing in this hypothetical asset with 15% expected returns and 10% standard deviation that follows a gaussian distribution. This means that at any given year, you can expect that there is a 68% chance your investment returns will be between 5% and 25%.
To wit, below is an illustration that if you throw a dart at random, your dart will land on the blue zone with a chance of 68%. You will miss the blue zone and land on the red zone (for better or for worse) with a probability of 32%.
And throwing a dart is akin to seeing the returns for a given year.
Now this 68% probability of returns between 5% and 25% in a given year. Easy. But we often care about making money. That means, if we throw a dart, how likely it is that we get a positive returns (>0%) in a year given that expected returns is 15% with a 10% standard deviation?
That number is 93%.
Yes, with the same assumption (expected returns of 15% with 10% deviation), we can expect that if we throw a dart, it will land on the blue zone 93% of the time! In other words, there is a 93% probability that your investment will have returns greater than 0% in a given year.
Think about it, this signals that it is not a bad investment overall. You stay invested for 10 years, you only get 1 bad year. The remaining years are wonderful.
Now let’s have the exact same asset but we shorten the time span
It’s still the same asset. The expected returns is still the same at 15% per annum and the deviation is also still the same at 10%.
But, what is the probability of the asset having returns (more than 0%) over one minute?
We can compute this and the answer is 50.17%. To wit, you can look at the expanded illustration below that illustrates the probability of success if we shrink the timeframe from 1 year to 1 minute for the exact same asset.
What the illustration above shows us is that if we throw a dart at random every minute, the dart only needs to land at the blue zone 50.17% of the time so that the asset can have an expected return of 15% with 10% deviation.
In the Indonesian stock exchange, the market is open for 5 hours and 20 minutes. This means that for the given asset, you will have:
165 minutes that are winning
155 minutes that are losing
statistically speaking.
Now here’s the problem
The 1 minutes of losing is not equal to 1 minute of winning because people are generally loss averse.
1 minute of losing almost always carries more weight than 1 minute of winning. It is more emotionally draining to see a losing trade than it is more emotionally uplifting to see a winning trade.
That is why we might have a tendency to view that the asset that we are seeing is a bad asset because maybe in a day, you have the 155 minutes of losing upfront. And then we proceed to get angry or time the market or {insert other impulsive things we do} only to realise that our decision was made based on noise.
All you have to do is to look at the returns on a less frequent basis. And you will find a more useful signal whether your asset is performing well or not.
Taking it personally
There is one thing that I find super encouraging from this piece though.
We can always view ourselves as an asset. You can imagine that we would grow in terms of skill, intellect and other things. Over the long term, if our expected annual growth is 15%, if we shrink it minute by minute, we only need to “win” slightly over half of the time (50.17% to be precise).
That my friends, is why they always say:
Make small wins every day and you will see the benefits to your growth over the long run.
And just a reminder when you face a bad day:
It’s potentially just noise and randomness, putting you in the red zone once in a while.
It’s just math. It’s all there is folks.