The economics of consumption and investments
According to an economist, should you consume or invest more?
A guest post by our good friend and one of our earliest clients, who also happens to be a cool economist 😎
What is the point of economic theory?
The world of academia and economic theory is often very abstract. When we read academic papers, we are often frazzled by the amount of math symbols, equations, and jargons that we don’t even know how they are relevant to our day to day life anymore. This is ironic, because the academic world is supposed to advanced our understanding of the world and to help people live a better life. But how can we advance our understanding and live a better life through these breakthroughs if we don’t understand them and no one cares to explain them in human language to us?
This is my humble attempt to focus at just one small bit of economic theory, explain it in human language, and draw relevant takeaways that people can implement in their lives.
Why do we care about theory in the first place?
Economic theories rest on 2 big assumptions:
People are rational agents
People’s objective is to maximise their happiness (in the economic language, they call this utility)
What is the implication of these 2 assumptions?
People will make the most optimal decision.
Sounds good right? But is this realistic? Of course not. The biggest problem is that real people are not rational. We often end up making sub-optimal decisions for numerous reasons. For example:
After a long day of work, we succumb to eating a pint of Ben and Jerry’s ice cream and regret it the next day
We buy new clothes and electronic gadgets on impulse even though we don’t need them
We get ourselves overworked, working from 8am-3am daily; we complain about our lack of work-life balance but still stay in the job for the past 3 years
Does this mean economic theories are useless? It depends!
They are useless if you are using them to describe people’s behavior and predict how the economy would evolve
But, they are useful if you use them as a guideline to help you make optimal decision
And so the purpose of this blog post is to use an economic model to help us think about how we should make decision on how much we should spend our money on consumption versus investments, and how much we should work.
Making decision on consumption, investment, and work
When we make decisions on how much to consume, how much to invest, and how much to work, we usually rely on some sort of implicit (but definitely not robust) thinking, or sometimes we don’t even think at all!
Most people don’t think too much about how much they should work; their boss decides for them. If they have nice boss, they can enjoy some work-life balance. If they have not-so-nice boss, they tend to be overworked. A minority of people do choose to exercise personal liberty on choosing the kind of work-life balance they want. These are people who choose to resign from their intense job and move to a more relaxed workplace. Others may do the opposite: they take up side-hustles or choose to take up intense jobs.
When people think about how they should split their income into consumption, savings and investments, most people also do not follow a systematic rule. Some people use their “feelings”. Others follow a widely accepted (but often arbitrary, and of questionable optimality) rule such as 60-20-20: 60% on consumption, 20% on savings, and 20% on investments. Some “wealth advisor” will use some complicated method of calculations. They will ask you when you want to retire, how much do you want to spend monthly during your retirement, what is the price of your dream house, how many children you want, what is the estimated expense of raising your children, etc etc. Then they will calculate backwards and give you a magic number on how much you should save and invest (in the financial products they offer) in order to achieve that dream of “financial independence” and retiring by 50. Yahoo!
Now, why don’t we use the tools that our economist friends have developed? Ultimately, these tools are built on the assumption that people are rational and people will make the most optimal decision in order to achieve maximum utility.
A very simplified model
I will look at just a small portion of an economic theory called the Ramsey model. Please note that the real model itself is more complex. Do read up more on your own if you are interested. But for the purpose of this exercise, I will only look at a portion of the model and modify it slightly so that it is relevant to our day-to-day decision of consumption, work and investments.
The portion of the model I want to talk about is very simple:
People want to maximise their lifetime utility (happiness), but they have budget constraint
Here, you get utility (happiness) from material and non-material stuff. Material stuff means things you buy with money (we call this consumption). Non-material stuff means the good time you spend (we call this leisure).
Naturally, to maximise your utility from consumption and leisure, you can just have infinite amount of consumption and leisure. But the problem is, we can’t do that because we have finite amount of money and finite amount of time. This is what we call budget constraint.
One last thing. We also assume diminishing returns to consumption and leisure. This simply means that you are always happier to consume more and to have more leisure, but this increase in happiness gets smaller and smaller.
What on earth is diminishing returns?
An analogy for you: on a very hot day in Jakarta, it is 40 degrees Celcius out there. You are walking around, feeling very hot and sweating loads. You walked past an ice cream store and got yourself a scoop of ice cream.
The first bite makes you feel “Aah, this is so so good!” Your happiness level is up by a score of 100. The second bite is still very good as it cools down your hot brain and body. Your happiness level is up by 99 still. By the time you finish your 1 scoop of ice cream, you are very much cooled down already and you feel great. That last bite of ice cream is still good, but not as good as the first bite. So that last bite increases your happiness level by 70. Imagine you order a second scoop, a third scoop, …, until a twentieth scoop.
By the time you eat your twentieth scoop, you are most likely so full of sugar that you don’t want to eat any more ice cream for the next month. That twentieth scoop probably does not give you extra happiness anymore. See how the increase in happiness goes from 100, 99, 70, and reaches 0? This is called diminishing returns.
After a good ice cream break, let’s go back to our objective: maximise utility subject to budget constraint
Let’s now look at some math!
Recall:
People want to maximise their lifetime utility (happiness),
But they have budget constraint
Translating this into math language,
People want to maximise their lifetime utility:
People have budget constraint
Decisions, decisions!
From the above, note that there are a few decisions that you have to make:
How much to consume today c_t
How much to work today h_t
a. How much to save and invest (b_{t+1}, k_{t+1}), which will affect how much you can consume tomorrow.
b. How much to allocate between government bonds b_{t+1} and equity investments k_{t+1}
Decision 3b: bonds or equity?
Let’s first look at the last decision (decision 3b). How should you choose between saving through government bonds or equity investments?
Caveat: here I am extracting away the element of risk, just to make things simpler. Maybe I will introduce more complexity and talk about portfolio allocation theory in a separate post if you guys are interested :)
The simplest rule to decide is just to compare the returns from government bonds (r_t^b) with the returns from equity investing (r_t^k).
If r_t^b > r_t^k , then you should just save through government bonds
If r_t^k > r_t^b , then you should just save through equity investing
But what about risk? Even though historical data shows that equity can give higher returns, it is also more risky. There is a chance that I can get higher returns, but there is also a chance that I will lose money.
You are right indeed. There are ways you can incorporate risk when deciding how much you want to allocate on bonds versus equity — this is the subject of portfolio allocation theory. Here I will show you one possible simple way to do so.
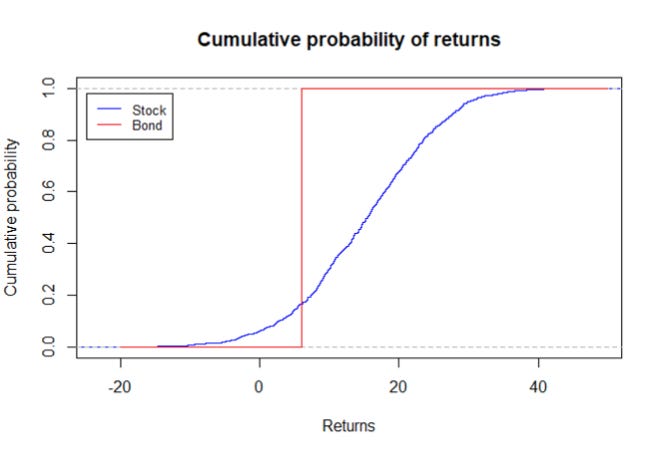
Let’s say you have an option between government bond and stock with the following returns:
From the cumulative returns probability above, we can see that there is an approximately 15% chance that my investments in equity will generate lower returns than the government bond. So I may want to construct my investment portfolio as such: 15% in government bonds and 85% in stocks.
Note that this allocation may change depending on the returns structure as shown in table 1. If you have bond that can generate higher returns, this will shift the red line to the right. Hence you may want to allocate more of your funds to bond. Conversely, if the mean returns to equity is higher or the standard deviation is lower, you may want to allocate more funds to equity.
Solving the problem
Recall again the rational agent’s objective: maximise lifetime utility subject to budget constraint.
In essence, the objective is simple: we want to find the most optimal combination of consumption, work and savings for all time periods (not just today, but for each year you are alive) that will maximise your lifetime utility as shown in the equation (1).
Note that for simplicity, I have combined the equity and bond variables into a generic “savings” variable (a_t) and I also simplify the returns to be r_t.
This is also called a mathematical optimisation problem.
In the next section, I will show the technical mathematics of solving the problem. But here I will just show you the intuition.
Look at the picture above. Think of the purple curvy sheet as the level of your utility for different combinations of consumption and leisure. Think about x as your consumption level and y as your leisure level. Now, you want to find the combination of x and y that maximises your utility. From the graph above, essentially we want to find point A because that is the point where your utility is the maximum.
Suppose point A occurs at x=1 and y=0.5. This means that to maximise your lifetime utility, you should spend $1 per year (this is hypothetical, remember!) and spend half of your time working (12 hours a day).
After you solve the problem (Closing Remarks)
The mechanism of which we solve the problem is described in later sections (appendix if you will). But assuming you have managed to solve the math equation (maximising utility subjected to the constraints), you will arrive at the following conclusions:
If you could expect higher returns from your investments tomorrow, you will tend to consume less today
If you expect lower returns from your investments, you will tend to consumer more today
Therefore, assuming that we are all equally patient, economists would argue that it makes more sense for us to budget our investments accordingly based on expectations of our investment returns. Stretching the line a little bit as well, if a society wants to have their individuals to be more forward looking, there needs to exist an investment vehicle that can optimise returns for individuals. Otherwise, individuals would be more short-termist in preferring to consume all their money today rather than saving them for a rainy day tomorrow.
Appendix: Want to solve the problem?
For math geeks (skip this section if you are a normal human being)
For the math geeks out there, you may know that this is a constrained optimisation problem. The economists traditionally solve this kind of problem using the Lagrangian method. That is, we first construct the Lagrangian:
To solve the optimisation problem, we take the partial derivatives of the Lagrangian with respect to the decision variables (c_t,h_t,k_{t+1}). So here goes:
Combining equations (3) and (5), we get:
Combining equations (3), (4) and (6), we get:
Equations (7) and (8) essentially summarise how you should make decisions regarding consumption, work and investments.
Decision 3a: how much to save
Equation (8) will tell you how much you should save. So let’s look at it again:
Before you get confused, let me explain what each term means.
u_c(c_t,1-h_t) refers to your marginal return to consumption this period (this year). This means that if you consume c_t amount today, how much extra happiness will you get from consuming 1 more unit. Another way to interpret this: if you spend $1000 on consumption this year, how much extra happiness will you get from spending $1 more.
u_c(c_{t+1},1-h_{t+1}) refers to your marginal return to consumption next period (next year).
Equation (8) says that your marginal return to consumption today should be a multiple of \beta*(1+r_{t+1}) compared to tomorrow.
Recall: \beta is discount factor for the future (the higher the value the more forward looking you are) and r_t is returns at time t (from your equity and bonds).
Suppose \beta=0.9 and r_{t+1}=0.1, then \beta*(1+r_{t+1})=0.99~1.
This means u_c(c_t,1-h_t) = u_c(c_{t+1},1-h_{t+1}).
In other words, you should consume the same amount every year. Hence, you should save enough to ensure that you can have the same level of consumption every year.
Now suppose \beta=0.9 and r_{t+1}=0.2, then \beta*(1+r_{t+1})=1.08.
This means u_c(c_t,1-h_t) = 1.08 * u_c(c_{t+1},1-h_{t+1}).
Recall again that while your happiness is always increasing as you consume more, there is the law of diminishing returns? Which means this increase is getting smaller and smaller?
You want to make sure that the marginal return from consumption today is 8% higher than the marginal return from consumption tomorrow.
The figure above shows the graphical illustration. Because you want your marginal utility today to be 8% higher than tomorrow’s, it means you should consume c_t=2 and c_{t+1}=3
Now suppose \beta=0.9 and r_{t+1}=0.06, then \beta*(1+r_{t+1})=0.95.
This means u_c(c_t,1-h_t) = 0.95 * u_c(c_{t+1},1-h_{t+1}). Hence, you should consume more today compared to tomorrow.
Notice how your consumption today relative to tomorrow changes with \beta and r_{t+1}?
As \beta increases, you become more patient and your consumption tomorrow increases relative to today’s
As r_{t+1} increases, you can generate more returns tomorrow and so you should save more, hence reducing your consumption today
Decision 1 and 2: how much to consume and work
Equation (7) will tell us how much we should consume and work.
Essentially, we want to work and consume at a level such that the ratio between the marginal utility to leisure and consumption equals to our wage rate.
So when you have higher wages, you might want to work more because it will give you more income.
Closing remarks
Thanks so much for entertaining my geeky nature. If you’ve read thus far, I hope you can take some of these theories to help you make better decisions in your life.
Cheers!